To this point we’ve examined ECharts’ language features. What we’ve intentionally ignored so far are the fundamental semantics underlying the language. This section answers some of the questions that you may have been wondering about such as: When more than one transition can fire, which one is chosen? Can data be shared between peer machines? When are machines created and destroyed?
As described in Sections 3.5 and 3.6, there are two ways to execute an ECharts machine: (1) a machine’s execution blocks until a message arrives from the environment and (2) a machine method is invoked with a port and a message as arguments and, therefore, does not need to block. We describe the first mode of execution in more detail here. The non-blocking mode of execution is more complex so we omit its description for the sake of brevity.
Blocking execution of an ECharts machine proceeds as follows:
To understand the pseudocode above you should understand the distinction between active and enabled transitions. A transition is an active transition if its source state reference is satisfied by the machine’s current state. A transition is an enabled transition if (1) it is an active transition and (2) the transition’s guard conditions are satisfied. A firing transition must be an enabled transition. A port is an active port if it is specified by an active message transition. Each machine execution cycle, a message is removed from a currently active port. More discussion related to message dequeuing is found in Section 4.6. Transition re-evaluation is discussed in Section 4.2. The concept of transition priority is discussed in Section 4.5. The concept of port priority is discussed in Section 4.4. Other issues related to execution blocking are discussed in Section 4.3. More information concerning enabled transitions can be found in Section 4.8.1.
As described in Section 4.1, a transition is enabled when its source state references are satisfied and its guard conditions are satisfied. For reasons of efficiency the ECharts runtime does not re-evaluate all of a machine’s transitions for satisfiability after a transition fires. Instead it re-evaluates a transition’s source state reference and guard if (1) the machine in which the transition is declared was explicitly referenced by the previously firing transition’s target or (2) the machine is an ancestor of the machine in which the previous transition fired. This re-evaluation rule affects the ability to correctly share data variables amongst machines as discussed in Section 4.8.
The essence of ECharts machine execution described in Section 4.1 is that the ECharts runtime attempts to fire as many transitions as possible in response to receiving a message from the environment. Only when there are no more transitions to execute is the next message from the environment considered. This approach to scheduling CPU resources is not uncommon for real-time systems. It is known as “run-until-blocked” or “run-to-quiescence” scheduling.
The sequence of one message transition followed by zero or more messageless transitions is referred to as a transition sequence. Note that the transitions in a transition sequence may belong to different submachines, including a machine’s current or-state submachine or any of its and-state submachines. However, there are constraints that dictate which transitions are considered for firing in a message sequence. This topic is addressed in Sections 4.2, 4.4 and 4.5.
A transition sequence is uninterruptible in the sense that once it is initiated for a machine no other messages from the environment will be acted upon until the sequence completes. Furthermore, the scheduling granularity is at the level of the transition. That is to say, a firing transition is guaranteed to run to completion without interruption.
There are a number of advantages afforded by this scheduling approach. The biggest one is that there is no need for explicit concurrency control to enforce data integrity constraints. For example, a machine’s transition action that updates a data value need not take precautions to protect the data value from simultaneous update by other transitions belonging to the same machine. However, it is important to realize the extent of the protection afforded by scheduling applies only to actions associated with the machine itself. For example, if the aforementioned data value is accessed by other threads (other than the machine’s thread) then the usual precautions should be taken, for example using Java’s synchronized construct. Another advantage of this scheduling policy is that scheduling granularity is effectively controlled by programmer. The less time actions take to execute, the finer the scheduling granularity.
However, this scheduling approach also has potential disadvantages that go hand in hand with with its advantages: starvation and blocking. When a transition action executes for a long time, it effectively starves other transitions from executing. For this reason, it is important that the execution time of individual actions be as kept short as possible. Furthermore, when a machine’s action makes a external blocking call no other transitions in that machine can fire until that blocking call returns. For example, if a state’s entry action makes a blocking call to retrieve a value from an external database, then no machine transitions can fire until the blocking call returns. In some programming contexts extended external blocking does not not matter. However, when it does matter, then efforts should be taken to convert the (synchronous) blocking call to an (asynchronous) non-blocking call that signals its completion by sending a message from the environment to a machine port.
In message receive operations, the class of ports implicitly associated with timed transitions have higher priority than internal ports which, in turn, have higher priority than external ports. For example, this means that if a timed transition has expired and is ready to fire, and messages are waiting in the input queues of internal ports and external ports of message transitions that are ready to fire, then the ECharts runtime will fire the timed transition first. Here’s a simple example:

In this example, the timed transition expires immediately. However, the message transition is also enabled because a message was placed in the transition port’s input queue by the machine’s environment. Although both transitions are enabled, the timed transition is guaranteed to fire since its implicit port has higher priority than the message transition’s port.
Transition priority rules are discussed in Section 4.5.
An important advantage of ECharts relative to other Statecharts dialects is that ECharts provides programmers with a number of ways to control which transition will fire when more than one transition is enabled in a machine state. Section 4.4 discusses one such way based on relative port priorities. In addition, ECharts provides three rules to resolve relative transition priority. The three priority rules are applied in the order we present them here. If one rule does not resolve the priority between comparable transitions, then the next rule is applied.
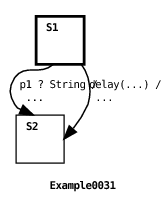
The first priority rule applies only to message transitions. If more than one message transition is enabled for a message from a given port, then the transition specifying the most specific message class will be chosen to fire. Here’s an example:
Both transitions in the machine are enabled because the message input to the port is an instance of both the Object and String classes. However, because the String class specified in the root machine transition is a subclass of the Object class specified in state S1’s submachine, then the String transition fires.
This priority rule is most often used as a way to override default behavior. One transition, intended to handle default behavior, specifies a general message class, and others are defined with more specific message classes in order to override the default transition when necessary.
In the context of an and-state or mixed-state machine, it is possible for a port to be referenced by transitions in more than one concurrent submachine. In this case, this priority rule is applied across all submachines guaranteeing that the transition chosen to fire will be the highest priority transition across all submachines. You should realize that this can lead to poor performance when there are many concurrent submachines since potentially all submachines must be inspected to locate the highest priority transition. In contrast, when an active port is shared amongst submachine elements of a machine array (see Section 3.11) then an element with an enabled message transition is chosen non-deterministically. In this case, there is no attempt to choose the highest priority message transition across all elements since this can lead to poor performance.
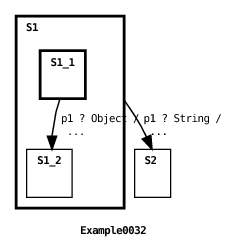
The second priority rule applies to all transitions for which the first rule fails to resolve priorities. The enabled transition with the highest priority is the transition with the most specific source state reference. This rule is a generalization of what is typically the only transition priority rule supported by other Statecharts dialects. Here’s an example:
And here’s the machine’s output:
In this case all message transitions in the machine are initially enabled. But the two transitions in the root machine have higher priority than the transition in state S1’s submachine because of the first priority rule discussed in Section 4.5.1. However, since the two root machine transitions have equal priority according to the first rule, then the second rule is applied. Since source state S1.S1_1 referenced by the second transition is more specific than the source state S1 referenced by the first transition, then the second transition has higher priority than the first transition under the second priority rule, so the second transition fires.
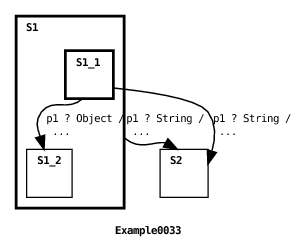
As mentioned earlier, the second rule applies not just to message transitions but also to messageless transitions. Here are two more examples.
Here is the machine’s output:
In the initial state, the root machine transition referencing source state S1.S1_1.S1_1_1 and the submachine transition referencing source state S1_1 are enabled. However, because the transition in the root machine references a more specific source state than the submachine transition then the root machine transition fires. Two more transitions are enabled once the machine transitions to state S2: the root machine transition referencing source state S2 and the submachine transition referencing source state S2_1. In this case, the submachine transition is guaranteed to fire first because its source state is more specific than the root machine transition’s. Finally, the parent machine fires since it remains enabled after the submachine transition fires,
The second priority rule is useful for two purposes. One purpose is to override the default transition behavior defined for a machine source state. To do this the programmer defines additional transitions defined for particular source substates. This use of the rule is shown in the last two examples. Another purpose is to allow submachine transitions to fire before more general ancestor machine transitions fire. This supports the view of a submachine invocation being akin to a procedure call in a traditional language. This use of the rule is shown in the last part of the second example above.
When the TERMINAL pseudostate (see Section 3.10.2) is referenced by a transition’s source, then it is considered to be less specific than a reference to an actual machine state. The second priority rule also generalizes to join transitions (discussed in Section 3.4.2). In this case, each join transition branch reference must be less specific in order for the entire join to be considered less specific. The notion of source state specificity is formally captured by term coverage which we will not cover in this document in the interests of brevity. The curious reader is referred to [3] for more information.
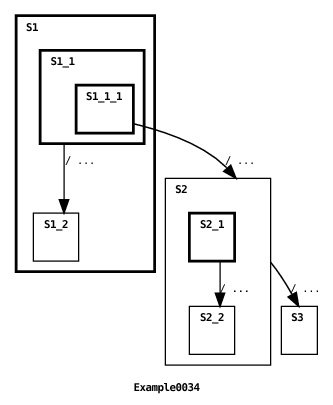
This last rule is applied when the previous two rules fail to resolve the relative priority of two comparable transitions. Like the source coverage rule discussed in Section 4.5.2, this rule applies to all types of transitions: timed, messageless and message transitions. When the source states references of two transitions are identical, this rule gives highest priority to the transition defined in a higher-level machine (or, if you prefer, a shallower depth machine). Here’s an example:
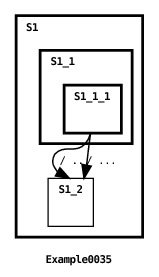
Here’s the machine’s output:
In this example both transitions refer to the same source state, namely state S1.S1_1.S1_1_1. In this case, the application of the transition depth rule guarantees that the root machine’s transition fires (see Section 6.4 for an explanation of the graphical depiction of this transition), since the root machine depth is shallower (depth 0) than the depth of the submachine defined for state S1 (depth 1).
The motivation for using this rule is to override submachine behavior. If a programmer would like to alter the behavior of a particular submachine’s transition, then a transition in an ancestor machine can be defined to reference the same source state and, optionally, the same target states as the submachine transition. This priority rule ensures that the ancestor transition will fire instead of the submachine’s transition.
In Sections 3.5 and 3.8 devoted to receiving and sending messages, we discussed how an external port maintains an input queue into which messages from a machine’s environment are enqueued. In Section 4.4 we discussed how dequeuing messages from timed transition ports has higher priority than dequeuing messages from other message transition ports. In this section we discuss two other issues related to dequeuing messages. The ECharts approach to message dequeuing attempts to balance two conflicting desires: (1) to never unintentionally lose messages from the environment and (2) to not overly burden the programmer. These two issues are addressed, in turn, in the next two sections.
The ECharts runtime model guarantees that no messages from the environment are unintentionally lost. The justification for this is simply that in most reactive programming domains, it is unacceptable to unknowingly lose a message. This aspect of ECharts distinguishes it from other Statecharts dialects that typically allow a message to be lost if it is not explicitly handled by a machine.
Here’s how ECharts ensures that messages are not lost: if p is an active port (see Section 4.1), then the ECharts runtime may dequeue a message from port p. Furthermore, if a message is dequeued from port p, then the machine must fire some message transition for that message, otherwise an exception is raised. Here’s an example:
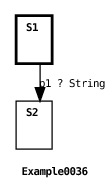
Here’s the machine’s output:
In this example, the machine’s environment enqueues an Integer instance on port p1’s input queue. However, the machine only defines a message transition for a String instance on p1, so the ECharts runtime raises an exception that is caught by the environment. If there had been an additional message transition for p1 that specified the Integer class or the Object (super) class then no exception would have been raised.
Having seen how unhandled messages are treated in the previous section, you may be asking yourself if it is necessary to add message transitions to every machine state for every message class anticipated on every port. The answer to this question is an emphatic: No. This would be an unreasonable burden on the programmer. Furthermore, it would obfuscate a machine’s logic. Instead, ECharts provides programmers with a facility to implicitly defer dequeuing messages from a port until the programmer explicitly declares a machine’s readiness to accept a message from the port. The way this is accomplished is very simple: if a port p is not active (see Section 4.1), then the ECharts runtime will not dequeue a message from p. Only when the machine arrives in a state where p is active may a message be dequeued from p. If a message is dequeued from p then the machine is obliged to fire a transition for that message. Here’s an example:
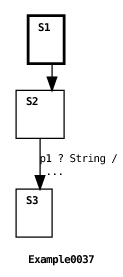
The example shows the machine environment enqueuing a message on port p1. However, the initial state of the machine does not include transitions specifying p1 so the message remains enqueued on the port until the machine reaches state S2 where there is a transition specifying p1. Since this transition specifies a String message then it fires and the machine completes its execution.
In the interests of conserving memory, ECharts machines are created only when they are needed and they are destroyed when they are no longer needed. This section explains in more detail what is meant by “needed” and “no longer needed.”
The root machine is created by the machine’s environment, as we have seen in many of the previous examples. However, submachines can be created in one of three ways: (1) If a submachine does not already exist then it will be created when it becomes part of a machine’s current state. (2) If a submachine already exists, then it will be re-created if its parent state is explicitly referenced as a target of a firing transition, and no sub-states of the parent state are referenced. (3) Finally, a machine array element can be created using the NEW pseudostate as discussed in Section 3.10.4.
Rule (1) ensures that a machine always exists when you expect it to. Rule (2) can be useful in order to explicitly reset submachine state. Here’s an example of both rules:
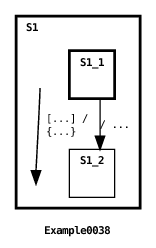
Here’s the machine’s output:
In Example0038, the submachine defined for initial state S1 is automatically created when the root machine is initially created. This is because S1 is the initial current state of the machine. The submachine transition fires printing out the initial value of field: 42. Then the parent transition fires (see Section 6.4 for an explanation of the graphical depiction of this transition). Since the transition target explicitly references S1 and no substates of S1, then S1’s submachine is re-created. The evidence of this is that, although the parent transition changes the value of the submachine’s field to 0, the value of submachine’s field printed when the submachine transition fires again is its initial value: 42.
The above example shows how rule (1) ensures that or-state submachines are guaranteed to exist when they are expected to exist. This rule generalizes to and-state and mixed-state machines in the expected way. Since every and-state is part of the machine’s current state, then all and-state submachines are guaranteed to exist during the lifetime of the parent machine.
To highlight the behavior of rule (2) consider the following example:
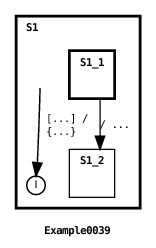
This example is identical to the previous example except that the root transition target references S1’s DEFAULT_INITIAL pseudostate, not simply S1 as before (see Section 6.4 for an explanation of the graphical depiction of this transition). In this case, S1’s submachine is not re-created since the transition references a sub(pseudo)state of S1. This is evident from the program’s output:
For practical purposes, rule (2) has been modified somewhat when applied to a machine array state. Instead of re-creating all the existing machine array elements, the array is cleared so that no elements exist in the array. Here’s an example:
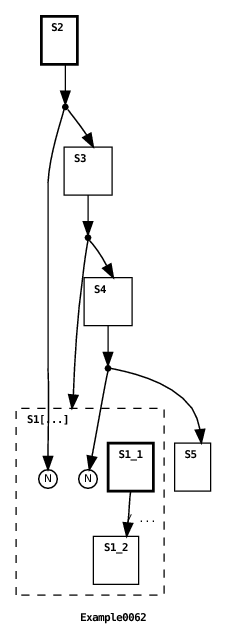
The machine output is:
In this mixed-state machine example, the first parent machine transition creates an array element in the and-state machine array S1. The next parent transition clears the machine array. The last parent transition creates another new array element. Note that S1’s array size is 1 so if the machine array hadn’t been cleared by the second parent transition, the third parent transition would have resulted in a runtime exception being thrown.
Apart from destruction as a part of re-creation (as discussed above in Section 4.7.1), a machine can only be destroyed once it enters a terminal state (the concept of a terminal state is defined in Section 3.10.2). However, a machine is not destroyed upon entering a terminal state; it can only be destroyed by an ancestor machine. In particular, the source state of a transition in an ancestor machine must explicitly reference the descendant machine’s terminal state in order for the descendant machine to be destroyed. Furthermore, the descendant machine isn’t destroyed until the transition’s actions have completed, thereby providing an opportunity to access the descendant machine’s methods or fields immediately prior to its destruction. Here’s an example:
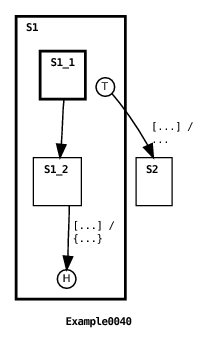
Here’s the machine’s output:
In this example, the submachine in state S1 transitions to a terminal state. Then the first root machine transition fires (see Section 6.4 for an explanation of the graphical depiction of this transition), printing the initial value of the submachine’s field variable, changing its value to 0, and then looping back to the DEEP_HISTORY pseudostate of the submachine. Since the submachine was in an terminal state, and since the root machine transition explicitly referenced the terminal state, then the submachine will have been destroyed when the transition fired. This means that the changed value of the submachine’s field variable will be lost when the submachine is destroyed. The transition’s target is state S1, so S1 becomes the machine’s current state again. As described in the previous section, Section 4.7.1, this means that a new instance of the submachine in S1 must be created. Since the newly created submachine has no prior state, the transition target DEEP_HISTORY pseudostate reference defaults to the submachine’s initial state S1_1. Once again, the submachine’s transition fires, moving the submachine to a terminal state. Now the second transition in the root machine fires, printing out the current value of the submachine’s field variable. Since the variable is defined in a newly created submachine instance then the initial field value, 42, is printed. You should also note that since the transition source references the submachine with the TERMINAL pseudostate, then the submachine will, once again, be destroyed. This time, however, the new current state of the machine becomes S2, so the submachine in state S1 is not re-created.
The same rule for machine destruction applies to elements of a machine array (see Section 3.11). In the context of a machine array, it is important for the programmer to remember to include transitions to destroy machine array elements that have arrived in a terminal state. Neglecting to do this will eventually result in the machine array reaching its maximum capacity leaving no opportunity for new elements to be added. Furthermore, this situation may also over-utilize memory resources. Also, as discussed in Section 4.7.1, it is possible to explicitly destroy all machine array elements at once, effectively clearing the array.
The destruction of a machine can be prevented by annotating the machine’s parent state with the nonterminal state modifier. As an example, see Example0022 in Section 3.11. This modifier informs the ECharts interpreter to treat the parent state as a non-terminal state even though it might be a terminal state. The nonterminal modifier does not affect machine re-creation as described in Section 4.7.1, however.
This section discusses the use of shared variables between machines. While data sharing may sometimes be necessary, internal ports should be used in lieu of shared data whenever possible. See Section 3.14 for details.1
To correctly utilize shared variables in transition guards one needs to understand the transition evaluation rule described in Section 4.2. Note that the rule’s two conditions imply that only ancestor and descendant machines may share variables referenced by guards; peer machines should not directly share variables referenced by guards.
To gain an intuition for the rule in the context of variable sharing here are a few examples. The first example illustrates an incorrect use of shared variables with guards. This will be followed by two examples showing the correct use of shared variables with guards.
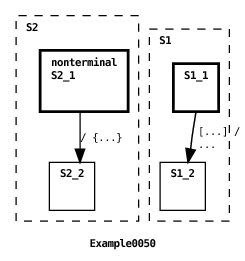
In the above example we show a failed attempt by a transition declared in the parent machine to trigger a transition in child machine S1 whose guard references a shared variable flag (see Section 6.4 for an explanation of the graphical depiction of this transition). The program produces the following output.
The parent updates the variable’s value but, because the program violates part (1) of the guard evaluation rule, the child’s transition does not fire. In particular, the parent transition does not explicitly reference S1 which means that S1’s transition guard is not re-evaluated after flag’s value is updated.
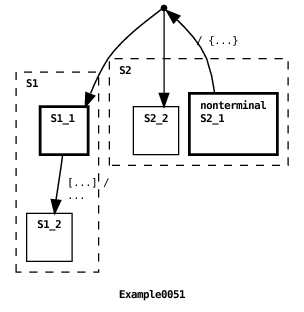
The problem with Example0050 is rectified in the example above. In this case, the parent machine transition explicitly references the child machine S1 via the target state reference S1.S1_1. In accordance with part (1) of the guard evaluation rule, S1’s transition guard is re-evaluated and the transition fires. The program’s output is:
Another example of correctly sharing variables referenced by guards is Example0029 in Section 3.15. In that example, the variable messages is declared in the parent machine and updated by transitions declared in the two concurrent child machines. The messages variable is also referenced by the parent machine’s transition guard. Since the parent is an ancestor of the child machines then, in accordance with part (2) of the guard evaluation rule, a transition firing in a child machine (that updates the messages value) will result in the parent’s transition guard being re-evaluated, which is the desired behavior.
A message transition specifies a port variable. Normally a port variable’s value remains constant during a machine’s lifetime. However, occasionally it is desirable to change a port variable’s value at runtime so the question arises: when is a transition’s port value re-evaluated? The answer is: the same rule that holds for the evaluation of guard variables described in Section 4.2. The same implications also hold, namely, that only ancestor and descendant machines may update shared port variables; peer machines should not directly update one another’s shared port variables.
Access permissions can be specified for ECharts machines, machine constructors and machine states. The permissions model used by ECharts is the same as that used by Java. There are four permission classes: private (currently unsupported for machines), public, protected (currently unsupported), and package (the default permission class if no permission class is explicitly specified). Machine pseudostates are assigned public access.
The permissions for machines, machine constructors and machine states are interpreted the same way as for Java class definitions, instance constructors, and instance methods, respectively.
Machine permissions and state permissions dictate submachine access permissions (see Section 3.13) and submachine state reference permissions in multi-level transitions (see Section 3.4.1). Machine permissions and machine constructor permissions dictate permissions for specifying and creating external submachines (see Section 3.1.2).
1 The shared machine modifier, present in ECharts versions less than or equal to 1.1 Beta, has been eliminated from the language due to the semantic complexity and performance overhead it entailed.